How to Make a Free Throw
I’ve mentioned before that I’m not that into team sports. My favorite sport is tennis. (Well, my favorite sport is combat robotics, but as far as commonly known, athletic sports, my favorite is tennis) But among the big-name team sports (soccer, football, basketball, baseball) my favorite is definitely basketball. All forms of football are too many people on too large a field, and baseball takes a seeming eternity to play. Basketball is condensed and easy to follow.
Anyway, it’s mid-March, and that means that it’s time for the college basketball tournament. For those unfamiliar, this is a single-elimination tournament between the sixty-four best teams of college varsity basketball teams in the U.S. The tournament will start with multiple games being played every day, to accommodate so many teams, hence the nickname March Madness. Over the next few weeks, there will be 63 games of basketball played. Or there would have been, if not for concerns over the coronavirus.
So now, there’re a bunch of basketball players with a bunch of free time. And I have an idea how they might spend some of it: just get real prepped for whenever they get to play again by practicing their free throws!

Free throws are broken down officially here, but essentially they are what happens when a player is wronged under the rules of the game, and they’re allowed to take an uninterrupted shot or two at the basket, getting a chance at easy points to make up for having their main gameplay attempt unduly hampered. Lots of times, even these free throws fail. I don’t play basketball, but when I asked a friend who does how anyone could miss a free throw, he said it mostly comes down to nerves. Fair enough. But free throws are seriously easy things to do, with practice, and I hope that if I can break down just how easy they are that I can provide some encouragement to the people who will be taking free throws.
So, I’m about to get a bit technical and start discussing some mathematical concepts. This is so that I can rationalize the act of taking a free throw, and explain it in terms that don’t rely on my own (largely uninformed) experience with taking free throws. In reality, when people play basketball, they don’t consciously run the math, they take actions by intuition. You don’t need to memorize any of this math, just use it to understand what, physically, a free throw is.
We’ve defined a free throw in terms of basketball rules, but in terms of physical rules, a free throw or any other non-dunk shot in basketball is a case of free projectile motion. That is, it is the sort of easy-to-model motion that is used to teach physicists and engineers how to model motion in the common way, using vectors.
Vectors are a mathematical concept, defined as something with magnitude and direction. For example, take a foot-long ruler. Its magnitude is twelve inches. Lay it on a table, and it will represent some physical vector. Turn it, and it will represent a different vector, as its direction has changed. Cut it in half, and it will also represent a different vector, as its magnitude has changed. But slide it across the table, without turning it, and it will still represent the same vector. Vectors aren’t where they are, just how much they are and how they’re pointed.
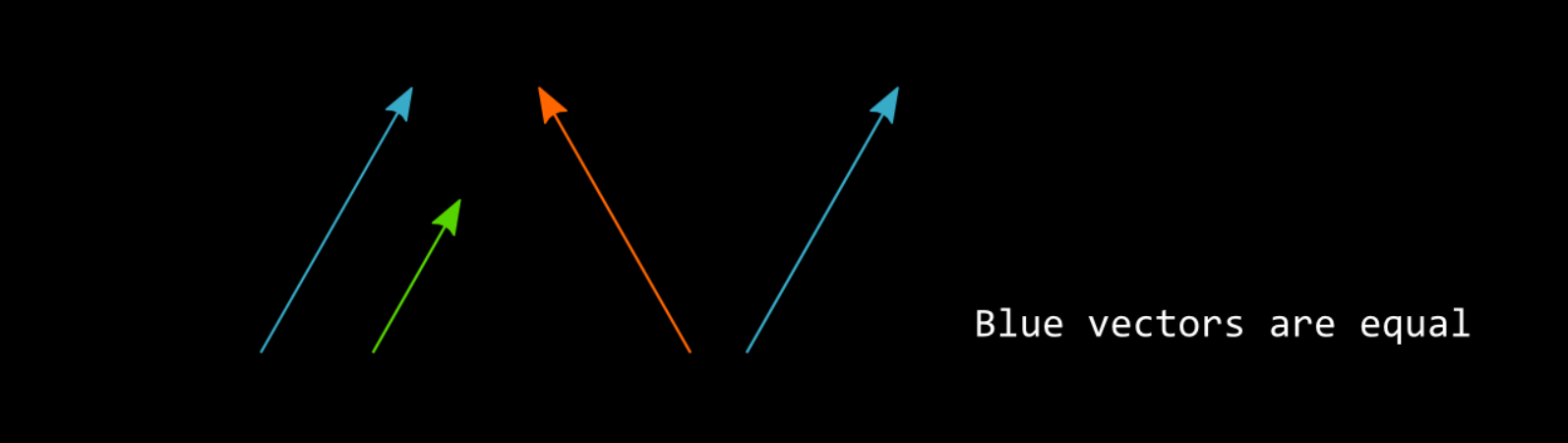
Vectors are useful because you can add them up or break them down into component vectors. If you place the beginning of one vector at the end of another vector, that will be the same as a single vector running from the beginning of the second to the end of the first. Likewise, any vector can be represented by a chain of other vectors strung end-to-end, so long as that chain starts and ends at the same relative positions.

Most usefully, you can break down any vector into vectors aligned with a useful reference coordinate system, as we will to mathematically describe a free-throw.
Taking a shot at-distance in basketball generally entails throwing the ball up higher than your head so that it falls down through a hoop that is higher up than most people, even most basketball players. Once you’ve thrown the ball, it is technically in free fall, accelerating toward the ground under the influence of gravity at a rate of 32.17 feet per second per second. That is, every second, it is moving 32.17 feet per second faster toward the ground than it did the previous second. That number will be very slightly different if you are above sea level, and completely different if you’re on some planet besides Earth, and air resistance plays a factor dependent on an object’s mass and surface area, but all that doesn’t matter here. The point is, as soon as you let it go, it begins to fall.
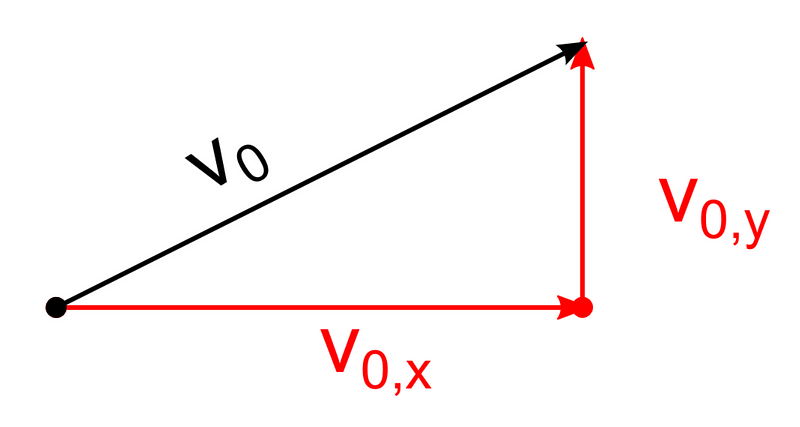
Now, let’s define a coordinate system. We’ll have one thing that goes horizontally from the player’s hand toward the basket (call this the x-axis, since that’s what it would usually be called) and another thing that goes vertically up and down (the y-axis) When you throw the ball, you push it in a direction both over toward the basket and up into the air. Using that vector breakdown method, we can describe that push as two pushes, one over and one up. The same is true of the initial velocity of the ball produced by that push.
The initial velocity is the velocity at which the ball is moving when it leaves the players hand and enters that free-fall projectile motion state. Velocities are vectors; they have magnitude (speed, in this case) and direction. The initial velocity can be broken down into horizontal velocity (v_x) and vertical velocity (v_y). For a basketball shot, the horizontal velocity should remain essentially unchanged until the ball hits something (hopefully the basket). It is affected by air resistance, of course, and a bit by something called Magnus force, which isn’t a proper force but an effect caused by the uneven distribution of air resistance over a spinning object, which thrown basketballs often are. These generally can be ignored in our case, as their effects on the path of the ball through the air are not very large. The vertical velocity will change quite a bit, though, because of that whole 32.17 ft/s² thing from earlier. So the ball is going to go across the court at a steady speed while going up slower-and-slower until, eventually, it’s going down faster and faster. The balls position along either axis can be given in the following equations:
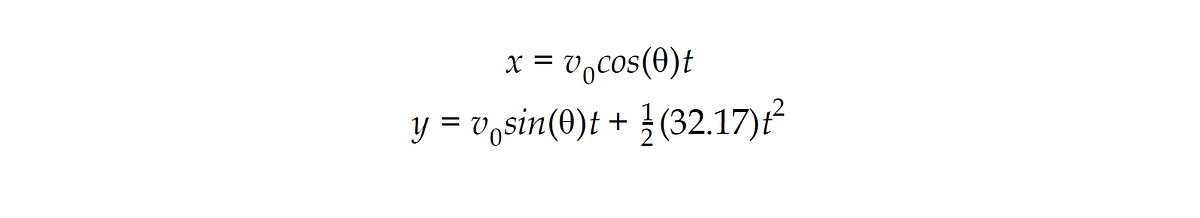
“ H ” is the height of the hoop, “ h” is the initial height of the ball over the floor. “v_0” is the initial velocity of the ball as thrown, and “ θ ” is the angle up from the horizontal that the ball was thrown at. “sin” and “cos” are sine and cosine, respectively. These are trigonometric functions, and you can read more about them here. The value “ t ” is the time, in seconds, since the ball has been thrown. A little algebra to solve the first equation for t and then substituting the result into the second equation gives us a third equation without t in it:
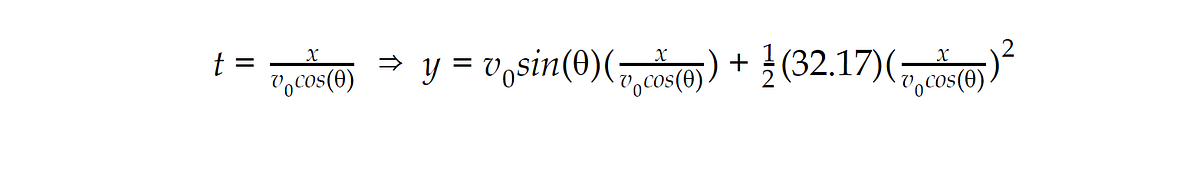
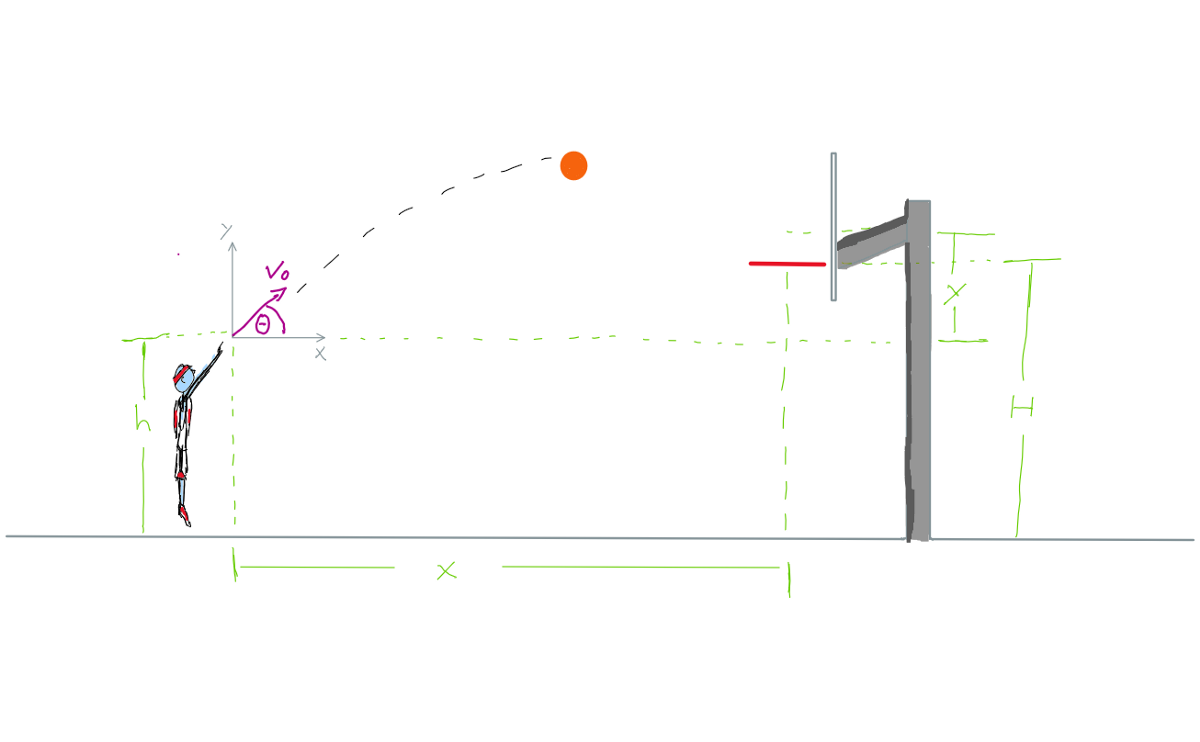
In the specific case of the free throw, that general basketball shot model of equations is constrained by a bunch of constants. The needed final value of x is 13 feet and 9 inches, or 13.75 feet. That is the distance between the free-throw line and the center of the basket’s rim, where you want to land to make that nice swish sound. The needed final value of y is a bit trickier since it depends on how tall you are and how high the ball is from the ground when you throw it. What we do know is that the basket is ten feet up from the court, and an NCAA men’s basketball is a little more than 9 inches across (or 0.75 feet), which means that as long as y = 10 feet -your throw height + 4.5 inches (0.325 feet, the distance from the ball’s center to its outside) then the ball will just clear the rim as it goes in. Throw height (called “h” in our equations) varies by player, but a good ballplayer will have generally consistent shot form and thus generally consistent throw height.
Taking these constraints into consideration, our equation from before becomes
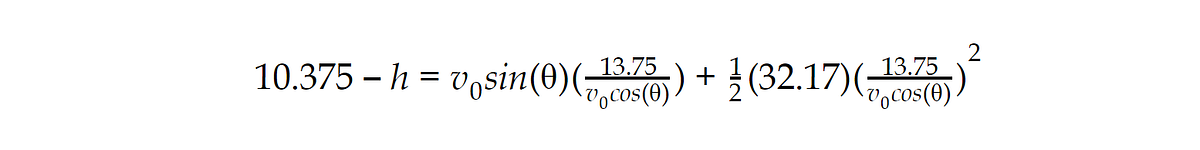
The equation is now all numbers except for 3 things, variables, that all change depending on player performance: h, depending on how high the player’s hands are; v_0, depending on how hard the player throws the ball; and θ, the upwards angle the ball is thrown at.

So what does that mean for you, a basketball player?
It means that there’s nothing stopping you from making a free throw but you. If you can make one free throw, then you just have to do exactly the same action to make every other. Your free throw, your unique combination of throw height, throw strength, and throw angle that puts the ball in the basket, is one single motion, to be done over and over the same way. Walking, writing, riding a bike, driving a car: these are all things many people can do, despite being much more complex, more difficult to mathematically describe, than throwing a perfect free throw. And people do those things without thinking about how, without worrying about any kinematic vectors or algebra; it’s all in their muscle memory. Practice, practice, practice your free throw, until you can make it without thinking, with your eyes closed, while holding a conversation.
Then, I dunno, get fouled a lot, I guess, and you’ve got the game half-won right there. Or you should, as long as my math checks out.
Note: if you came here looking for dynamics help, not basketball help, you should take a look at this paper I found, which delves deeper into the science of free throws. Their math model is a bit different than mine, but both are valid.






Member Commentary